谈祾灏：谐音理论在检验音程中的应用 3-2 180910

精彩回顾

谐音理论在检验音程中的应用3-2

文/谈祾灏

谈祾灏：2016斯坦伯格杯全国钢琴调律师职业技能竞赛全能金奖 调律、维修、整音赛项金奖 调整赛项银奖

二、琴弦的非谐性振动

1、琴弦的非谐性振动

前面我们所说的倍音是与基音成整数倍关系，而这种整数倍关系是在理想弦振动下才能实现的。这要求琴弦是固定两点由固体材料制成的“完全柔顺和均匀的细线”，但实际上钢琴琴弦并非如此。首先钢琴琴弦是由金属制成，存在金属刚性，具有抗弯曲力，并非柔顺的。第二点琴弦两端并非完全固定的，弦马一端的点必须有足够的振动才能把能量传递给音板。这些都使得它的实际振动长度短于理论振动长度，实际音高频率要高于理论音高频率。振动频率的计算公式如下：

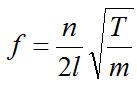
公式中：n为任意弦段振动频率的比值或对应的倍音次数；       

        f为琴弦的振动频率；

        l为琴弦的有效弦长；

        T为琴弦的张力；

        m为琴弦的单位长度质量。

那么在同一根琴弦上，其他参数不变，但琴弦由于琴弦本身刚性原因使得琴弦的振动长度l减小，那么振动频率f的数值必会增大。但是我们由该公式无法得出到底偏差多少，以及谐音实际振动频率。所以必须要加入偏差修正量(1+G),得实际弦的振动频率公式：

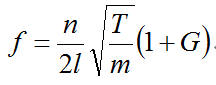
公式中G是因弦的刚性或力劲原因的修正值。

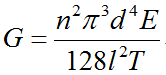
由此公式带入准确参数，即可得出弦振动以及各谐音实际振动频率。

同时，有公式可看出随着谐音次数n的增加，最终得到实际振动频率偏差值也会越大。也就是说，谐音次数越高，越不和谐。

由上述可知，为什么“倍音”在实际意义上与“基音”不成整数倍关系的原因，这也是本文前面强调的“倍音”与“谐音”的区别。因为实际意义上琴弦的分段振动，发出的谐音都比理想数值偏高。并不如倍音与基音那样谐和。所以真正意义上的倍音，在同一根琴弦上并不存在。实际弦振动的谐音都是不谐和的谐音，具有不谐和性。

2、钢琴调律曲线

前面所说谐音受琴弦的非谐性振动影响，会出现相比理论数值偏高的现象，那么必然会对听觉调律作业产生影响。听觉调律是通过辨别吻合谐音之间“拍”的快慢，来确定所调音的音高的。所以谐音的不谐和性也是我们所说的钢琴调律曲线产生的原因。

钢琴听觉调律从基准音组向高音区低音区扩展的基本方法是“调律八度平移法”。那么我们所判断的也就是八度两个音的吻合谐音。例如，当八度上行调律作业时，参照音是下方音，被调整的音是上方音。那么它们的吻合谐音参照倍音列可得，下方音为2、4、8、16次倍音，上方音为1、2、4、8次倍音。下方音的倍音次数是上方音的2倍。但我们还需要引入偏差量Δ，

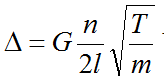
可理解为谐音实际数值和理论数值相比较的偏差。那么被调整的音实际获得的频率为：(2+Δ)f，比理论数值2f高出Δf。当调低音时，与上行正好相反，被调整的音是下方音，可得公式

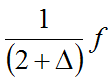
偏差量Δ为分母，那么最终数值便会比理论数值偏低。由公式

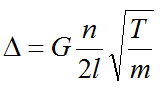
可知，随着音高上升，那么偏差量Δ数值就越大。那么就表示，随着音高上升，实际获得频率(2+Δ)f数值就越大。那么体现在曲线表上高音实际振动频率就是呈现上升趋势，并且音高越高上升量越多。同理随着音高下降，Δ越大。那么公式

最终数值就越小。体现在曲线表上音高实际振动频率就是呈现下架趋势，并且音高越低下降越多。