梁志伟、肖巍、欧阳雁、谢志文：树种对钢琴音板有限元模型基频的影响2-2结果与讨论 240429

树种对钢琴音板有限元模型基频的影响2-2结果与讨论

文/ 梁志伟¹，肖巍¹，欧阳雁²，谢志文²

（1.广州市珠江钢琴集团股份有限公司，广州510388；

2.华南理工大学理学院声学研究所，广州510641）

图文处理/ 霸拓编辑部

百花齐放、百家争鸣是学术的基本态度。作为学术平台，霸拓推送（并不代表认同）能引发思索的文章。

3结果与讨论

钢琴音板是用木质材料做成的，虽然大自然中树种的类型繁多，但并非所有的树木都符合制作钢琴音板的基本要求，现选取云杉、松木、花旗木、山毛榉、核桃木、轻木和白蜡木等7种常见的树种作为钢琴音板的用材，它们的材料属性如表1所示。

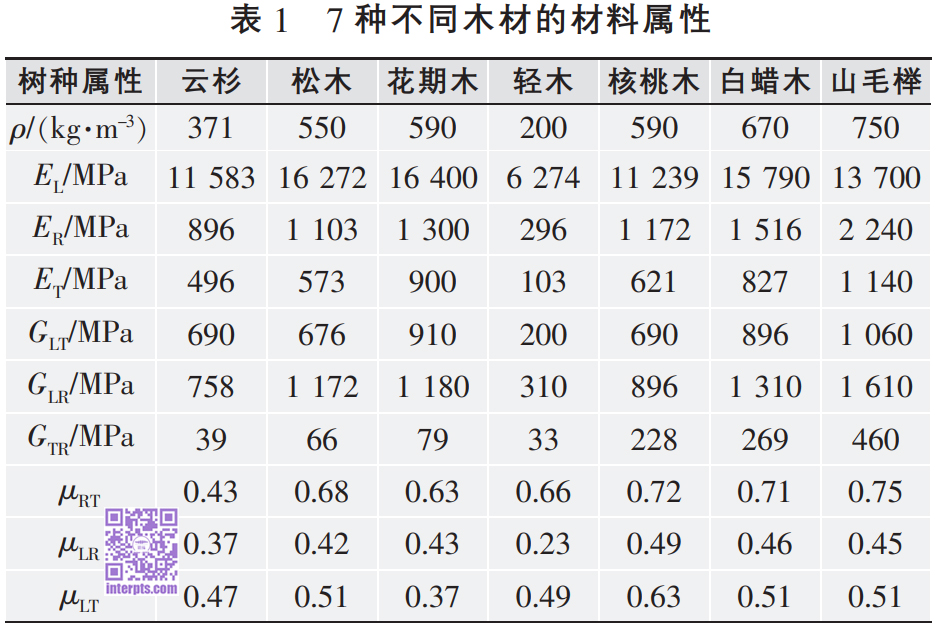
注：E，G和μ分别代表弹性模量、剪切模量和泊松系数；L，R和T分别表示木材的顺纹方向、水平径向和水平弦向。

在实际工作状态中的钢琴音板上，人们不仅装备了共振板、肋木和马桥等部件，还安置了悬挂于其上方的琴弦和用于固定支撑它的铸铁结构，为了集中研究音板的振动模态，笔者将取不带琴弦和铸铁结构的钢琴音板作为研究对象。

另外，在跟据分析对象的实际结构建立几何模型之前，必须进行简化处理。如何保证简化处理的合理性是后续分析的关键，不同的结构和不同的分析要求都会造成模型的简化方法不尽相同。笔者对钢琴音板作了如下的简化处理：

（1）钢琴音板主要包括了肋木和共振板，而实际的共振板拼接而成后，其表面具有一定弧度，在ANSYS中将采用板-梁结构建立这一模型；

（2）板和梁模型的简化：共振板的背面分布着大小不一的11根肋木，笔者采用Beam189属性的梁模拟音板上的肋木，采用Shell93属性的矩形板模拟钢琴音板的共振板；

（3）肋木的几何位置取在与音板纹理互相垂直的方向，这与实际情况的误差在5°以内；

（4）实际的肋木是两边呈凹槽状的不规则条状物，为了建模的方便，取肋木的厚度大小一致；

（5）约束的简化：实际中，工作的钢琴音板四周是通过螺钉锁紧固定在外围的铸铁支架上的，笔者采用音板四周边界固支的边界条件来近似反映钢琴音板的实际约束。

简化后的钢琴音板网格模型如图1所示。采用此网格模型进行计算，可得到各个树种的各阶振型模态云图和对应的频率。图2为核桃木的一阶振型模态云图和固有频率。一阶振型表现为音板前后方向的振动，其中主振型出现在音板的中心位置。表2为各个树种音板的基频，图3为树种-固有频率条形图。

:

图1：音板网格模型

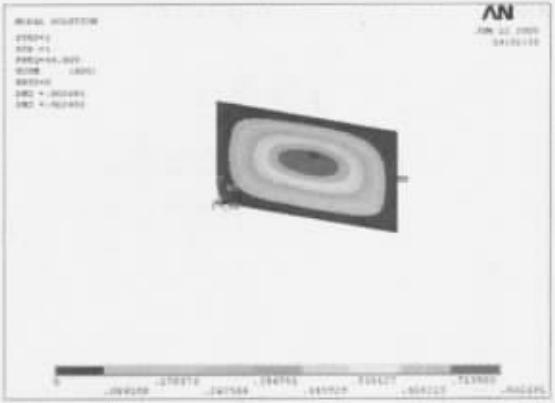
图2：核桃木一阶振型模态云图和固有频率

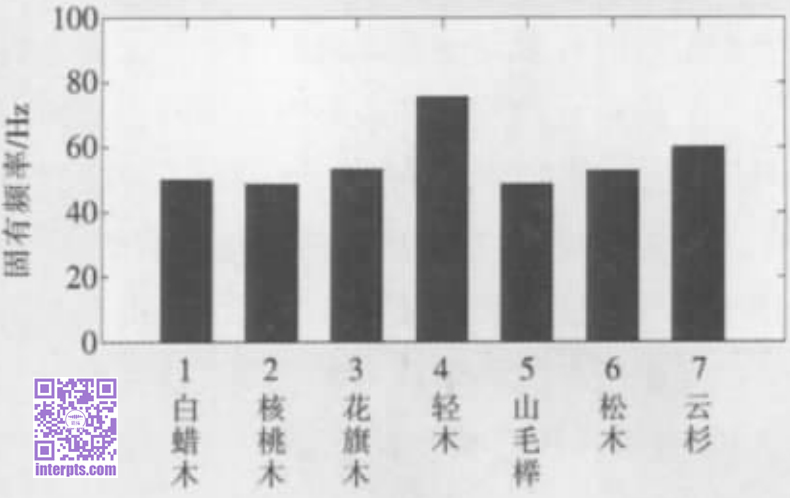
图3：树种类型-基频频率变化曲线

表 2 树种类型与音板基频对应关系

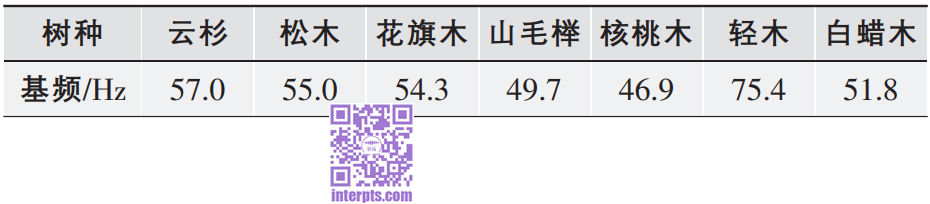
从表2和图3可看出，用材选取轻木时，音板的基频最大；而选取核桃木和山毛榉作为用材时，钢琴音板能够获得最小的基频，不同的树种对钢琴音板基频的影响是明显可见的。

根据各向同性材料的物理参数与振动基频之间的关系可知，弹性模量越大，基频越高，而密度越大，基频越低。从表1可知，在所研究的上述7个树种中，轻木的密度最小，但其弹性模量和剪切模量也最小，而泊松系数则介于中间值。核桃木的密度、弹性模量、剪切模量和泊松系数均取中间值。由此可见，基频与树种的密度、弹性模量、剪切模量和泊松系数均有关，要得到理想的基频，必须综合考虑这几个参数的影响，统一进行计算。

参考文献

[1] 刘镇波，刘一星，沈隽，等.云杉木材钢琴共振板振动特性的研究[J].北京林业大学学报，2008，30（5）：129-133.

[2] 刘镇波.云杉木材共振板的振动特性与钢琴声学品质评价的研究[D].哈尔滨：东北林业大学，2007.

[3]SUZUKI H.Vibration and sound radiation of a piano soundboard[J].Journal of Acoustical Society of America，1986，80（6）：1573-1582.

[4]GIORDANO N.Simple model of a piano soundboard[J].Journal of Acoustical Society of America 1997，102（2）：1159-1168.

[5]BERTHAUT J，ICHCHOU M N，JEZEQUEL L.Piano soundboard：structural behavior，numerical and experimental study in the modal range[J].Applied Acoustics，2003，64：1113-1136.

[6]GIORDANO N.Mechanical impedance of a piano soundboard[J].Journal of Acoustical Society of America 1998，103（4）：2128-2133.

[7]王勖成.有限单元法[M].北京：清华大学出版社，2003.

[8]蒋孝煜.有限元法基础[M].北京：清华大学出版社，1984.

[9]邓平凡.ANSYS10.0有限元分析自学手册[M].北京：人民邮电出版社，2007：68-386.

[10]傅志方.振动模态分析与参数识别[M].北京：机械工业出版社，1990.