陈重生：钢琴调律-钢琴调律方法-宽、窄音程调整的方法 240101

钢琴调律

钢琴调律方法-宽、窄音程调整的方法

文/陈重生 （南京艺术学院）

图文处理/ 梁锐祥（星海音乐学院）等

来源/ 中国轻工业出版社

百花齐放、百家争鸣是学术的基本态度。作为学术平台，霸拓推送（并不代表认同）能引发思索的文章。

从上述得知所谓宽音程、窄音程是相对纯律音程而言的，那么它们的调整和确认自然与纯律音程有关。我们知道纯律是一种“自然律”。纯律之所以是自然律，因为它各个音程的音程比与构成音程的律音的倍音列，相互之间有着不可分割的联系。详见表14—2和图14—1。

表14—2    纯律大音阶音程关系表

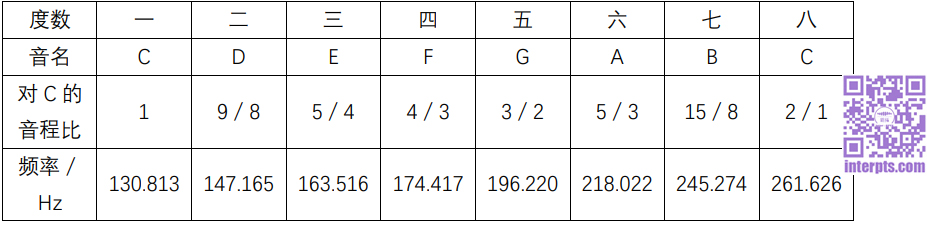
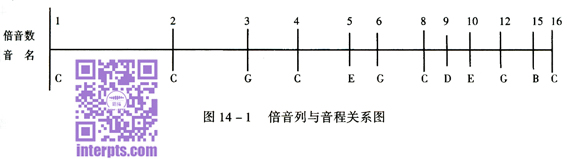
    从表和图中可以看出，纯律音程的音程比与倍音的比相同。如，五度的音程比为3：2，倍音列中第2倍音与第3倍音音高之间的距离刚好是一个五度音程；四度的音程比为4：3，倍音列中第3倍音与第4倍音音高之间的距离刚好也是一个四度音程……

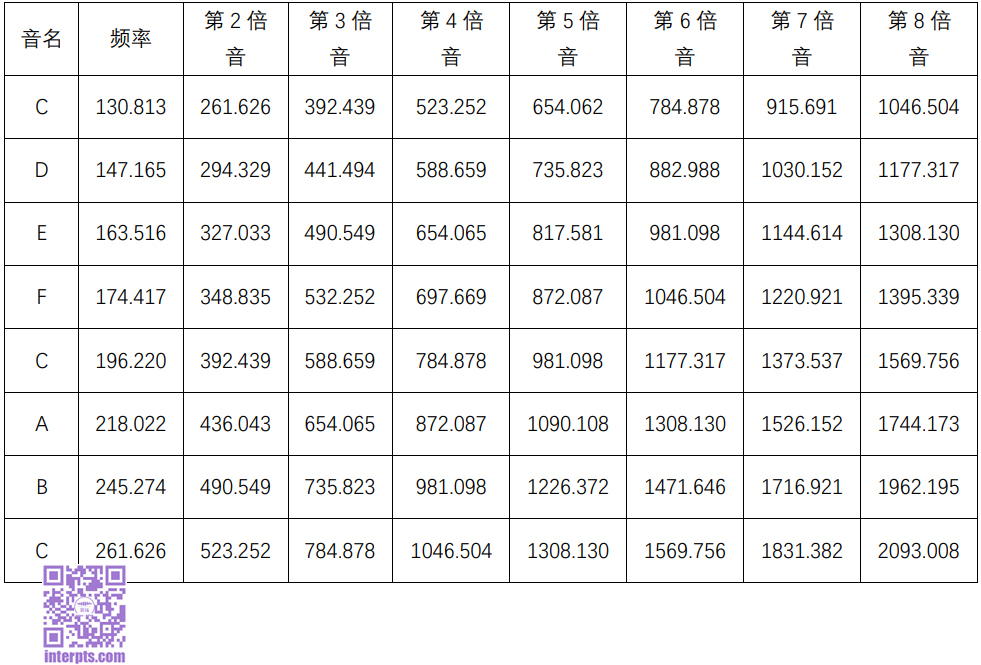
    由于，弦振动产生的音是复合音，均由基音和一定数量的倍音构成。因此，弦振动产生的音都按其基音频率构成倍音列。我们仍按以下表中纯律大音阶的每一个音罗列它们的倍音列(表)。表中，相同边框里的频率数是相等的。我们将这种倍音次数不等而频率数相等的倍音称为“共同倍音”。如，C—G五度音程的共同倍音是C音的第3倍音和G音的第2倍音；C—E大三度音程的共同倍音是C音的第5倍音和E音的第4倍音……可以认为纯律音程的共同倍音的音高是相互吻合一致的。或者说共同倍音音高吻合一致的音程是纯律音程。同时，我们还可以发现纯律音程的音程比与共同倍音的次数相同。如，五度音程的音程比为3：2，它们的共同倍音分别是第3倍音和第2倍音……当然，音程比两个数值不能与共同倍音的次数等同起来看。因为它们各自的意义不同。但它们却有千丝万缕的联系。如下式：

纯律五度音程的共同倍音音高相等得：

    C × 3＝Gx2

    C÷G＝2÷3    (1)

    G÷C＝3÷2    (2)

    C＝G×2／3    (3)

    G＝C×3／2    (4)

    式(1)可认为五度音程时C音和C音的频率关系，即， C音高为2(130．813Hz)  时,C音高就为3(196．220Hz)。

    式(2)可认为五度音程时音程的距离，即C音相对C音的音程比为3／2或196．220／130．813。

    式(3)或式(4)是已知五度音程其中一个音高，求另一个音高的公式。式(3)是求根音(下方音)的公式，式(4)是求冠音(上方音)的公式。

同理，可以其他音程的共同倍音相等的关系推导出同样的结果。

在对钢琴实施平均律音律的调整，就是利用纯律音程与倍音的关系和平均律音程与纯律音程的关系来实现的。