【德】钢琴制造-钢琴制造经验-弯曲力计算 弯力矩 190128

【德】钢琴制造

译/ [台]陈喜棠

注/ 周军 [易弹乐器（上海）有限公司]

图文处理/ 梁锐祥（星海音乐学院） 等

资料提供/ 霸拓

百花齐放、百家争鸣是学术的基本态度。作为学术平台，霸拓推送（并不代表认同）能引发思索的文章。

弯曲力计算

前节述及框板支架中间受压力之状况。但钢琴板架并不完全单受压力之作用，仍常同时生弯力作用。为使能计出受压力和弯力合并之大小，首先须明了纯弯力之计算。现在先行叙述之。钢琴框板支架少有单受智力之情况，故本节仅举简单之例，使读者对此问题易而明了。

弯力矩

杠杆上常有一或多数垂直负荷之力，致生一种弯应力。图86指出一杠杆，一端为可转动之承座，杆之另一端则施以垂直之力1000公斤。此力使杆铙O点转动，形成一种旋转运动。此种力之作用构成一种扭力矩。此种状态为单面受力之杠杆，故可利用杠杆定理。此扭力矩是系于力之大小和其转点之距离·，此距离愈长，扭力矩愈大，又所施之力愈大，扭力矩亦愈大。故扭力矩之计算为力舆力臂距离之乘积(M＝力×力臂)。由图可看出，以同等之力，但只有一半杆臂，力矩亦只有一半。

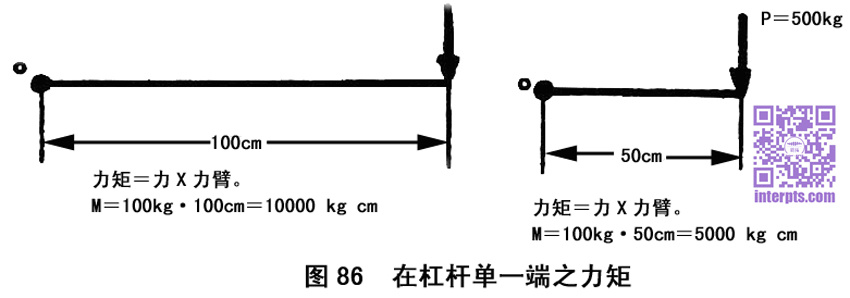
图87指出有两支承座之杠杆。一力P垂直施于杠杆中央。杠杆不能因受力而断裂。故杆上所生之力矩须有相对作用之同等大小力矩，始能平衡。此杆无扭力矩，乃系受弯应力，而构成弯力矩。设此杆被施于中央之力生剪切作用，即可求出此弯力矩。杆上一半力施于左端承座A至中央之力臂，另一半力则施于右端承座B至中央之力臂。在杠杆中央产生之力矩为最大。接近承座方面，因距离逐渐减短，力矩亦随之减小。至支承座端，力矩为零。力矩由中央至承座方向之减小指出产力矩面积。支架之尺寸应以最大之力矩计算。(上述情形是在中央)。

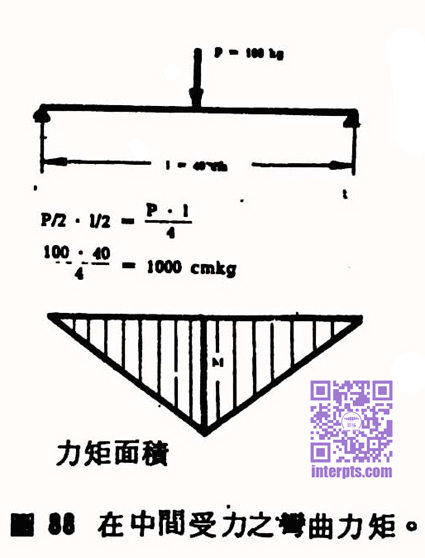
    如上所述，臂力矩系由一半力所产生。此力施于力臂上为一半支承距离。原公式为M＝力×力臂，现在以P₂之力，并一半之杠臂代替，故M=P·ℓ/4。在本例中计出此弯力矩为1000kg／cm。

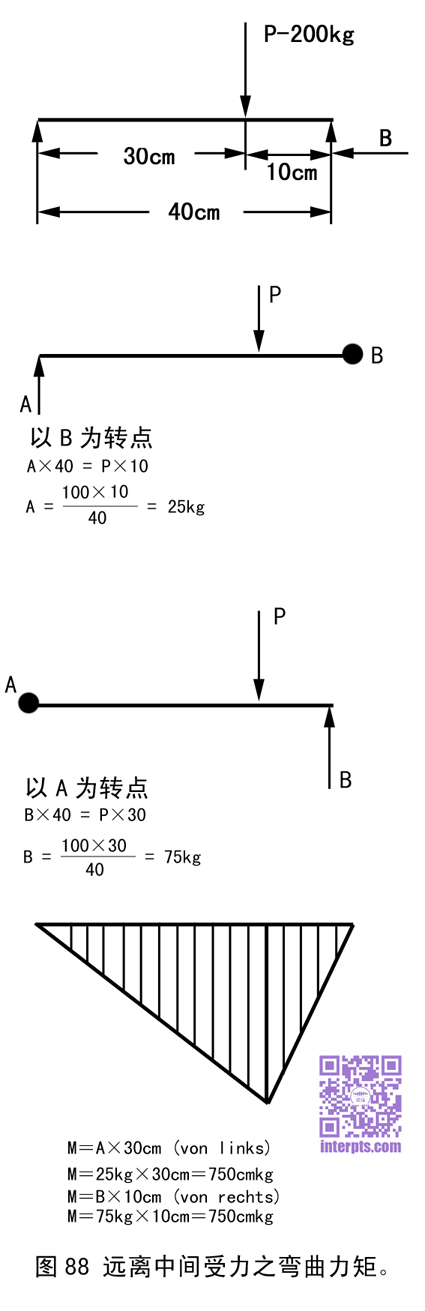
杠杆上所受之力致生弯力矩者，不单发生于两承座之中央。图88指出一杠杆所受之力为远离中央者。此种情形，不能将其力半分计算，因为着力点不在AB承座同等距离上。故须先计算各占之部份。设杠杆在B点可以转动，此杆必须平衡，故向上下转动之力矩均须相等。向上旋转之力矩可用力A和杆臂ℓ＝40cm计出。向下旋转之力矩，可用力P和杆臂ℓ＝10cm计出。如果将此两力矩以等式列出，即得40×A＝P×10 。 P为100kg，而将上式倒转得： A=100X10/40=25Kg。施于A部份之力P为25kg。其余之力应施于承座B上，即75cm。设杠杆可在A点旋转，则亦可仿照A计出(参阅图89)。杠杆上最大之力矩亦必产生于着力点上。现在可将左右两边力矩同时计出。两边力矩必须相等。左边A以25kg计算，杆臂为由A至P之距离。求出之力矩为750cm/kg。右边可以同等方式计之(参阅图88)。

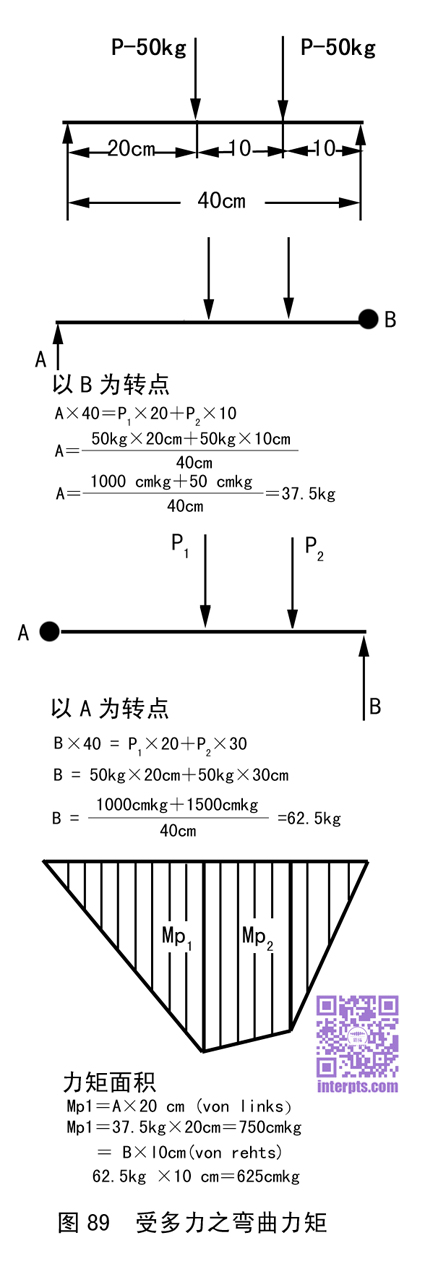
    杠杆上常多于两力以上之负荷。如图89指出一杠杆有两力之负荷。为求此杆之最大弯力矩时，首先亦需要算出在A和B两承座所受之力。兹再设B为转点。力A以40cm之杆臂向上旋转。力P₁以20cm之臂杆向下旋转，力P₂则以10cm之杆臂向下旋转。因此可定出一平衡方程式：A×40＝P₁×20＋P₂×10 。由上式计出力A＝37．5kg。 B以同等方式计算：B×40＝P1×20＋P2× 30，求出B＝62．5kg。

在P1之弯力矩，为力A×20cm杆臂，得750cm／kg。在P₂之弯力矩为625cm／kg。在图上之力矩面积可看出，最大力矩产生在P₁之位置。故必须以此弯力矩750cm/kg作为板架断面之计算。

注释：

1、力矩：力和力臂的乘积叫做力对转动轴的力矩。
即：M=F*L。式中M是力F对转动轴O的力矩，凡是使物体产生反时针方向转动效果的，定为正力矩，反之为负力矩。单位：在国际单位制中，力矩单位是牛顿*米，简称：牛*米，符号:N*m。

2、文中所示的各字母代表的含义与我们上学时所授的字母并不相同，文中的P表示的是kg，理论上应该换算成F/牛来进行计算；长度单位此处是cm，而我们则要换算成m。读者不用纠结于此，只要理解作者想表达的意思即可。

3、文中图86，少了和右边一样的p=500kg的已知条件。

4、力矩面积的图中，最下方应为：“图87 在中间受力之弯曲力矩”；计算式中，ℓ =40cm，p=100kg；数字不清，我们推测应是“M”。

5、图88中，p-200kg应为p-100kg。

6、图89中，在计算A的值时，50kg X 10cm应该等于500cmkg，而非50cmkg。